
OCCHIO...
ALLA FISICA



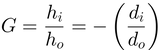





LA RIFLESSIONE DELLA LUCE
Quando un raggio di luce incontra un ostacolo che ne impedisce la propagazione, essa viene riflessa, proprio come accade a una palla da biliardo quando urta contro una sponda.
Questo è un fenomeno molto comune, infatti la maggior parte degli oggetti riflette una parte della luce che li colpisce.
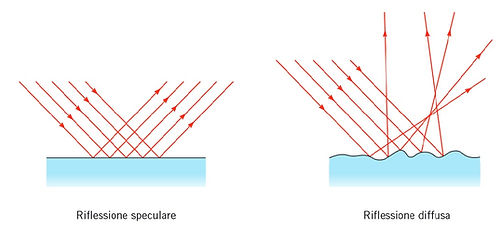
Ci sono, però, delle differenze nella riflessione a seconda del fatto che la superficie riflettente sia liscia, ben levigata o ruvida. Nel primo caso si parla di riflessione speculare: tutti i raggi riflessi sono tutti paralleli tra loro. Nel secondo caso, invece, la luce riflessa viene mandata in varie direzioni, originando una riflessione diffusa o diffusione.
Nella prima figura è possibile osservare la riflessione speculare della luce, mentre nella seconda è messa in evidenza la diffusione dei raggi luminosi emessi da una sorgente puntiforme. In questo secondo caso, ciascun raggio incidente si riflette secondo le leggi della riflessione, ma i raggi riflessi hanno direzioni che variano disordinatamente.
Di conseguenza, un osservatore che si trova dalla stessa parte della sorgente rispetto alla superficie riceve i raggi riflessi sempre, qualunque sia la sua posizione.
Per esempio, alcune superfici che danno luogo alla riflessione diffusa sono la maggior parte dei fogli di carta, il legno, i metalli non lucidati e le pareti dipinte con vernici non lucide.
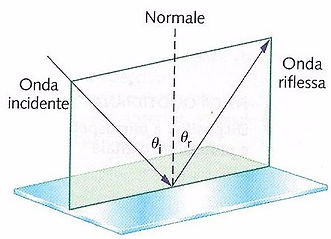
Se consideriamo, ora, una superficie piana e ben levigata possiamo caratterizzare il comportamento della luce osservando la figura a lato.
Disegniamo innanzitutto la retta normale, ovvero quella perpendicolare alla superficie riflettente nel punto di incidenza del raggio luminoso.
Rispetto alla normale, il raggio incidente forma un angolo ϑi, l’angolo incidente.
Analogamente l’angolo di riflessione ϑr è l’angolo formato dal raggio riflesso con la normale.
Si trova sperimentalmente che il fenomeno della riflessione segue due leggi:
PRIMA LEGGE:
il raggio incidente, il raggio riflesso e la normale alla superficie d’incidenza giacciono nello stesso piano.
SECONDA LEGGE:
l’angolo d’incidenza è uguale all’angolo di riflessione.
Nel nostro caso, grazie alla seconda legge, abbiamo quindi: ϑi = ϑr.
Il fenomeno della riflessione è alla base del funzionamento degli specchi.
Ogni giorno, ad ognuno di noi, capita di guardarsi allo specchio ed osservare la propria immagine riflessa. Vediamo, ora, come questo sia possibile.
Possiamo, innanzitutto, distinguere due tipi di specchi:
-
gli SPECCHI PIANI;
-
gli SPECCHI SFERICI.
SPECCHI PIANI
Consideriamo una superficie speculare piana dotata di potere riflettente, comunemente chiamata specchio piano.
Osservando la nostra immagine allo specchio, quello che possiamo notare è che essa è dritta, ha le nostre stesse dimensioni e ci appare collocata dietro lo specchio, ad una distanza da esso uguale a quella fra noi e lo specchio.
Ma perché quando ci guardiamo allo specchio e alziamo la mano destra, la nostra immagine alza la sinistra?
E perché, visto che c’è questo rovesciamento, la testa e i piedi non vengono rovesciati?
Ovvero ci chiediamo: perché lo specchio rovescia tutti gli oggetti da destra a sinistra, ma non dall’alto al basso?
Il problema, in questo caso, sta nella domanda. Essa, infatti, è tendenziosa. Vediamo perchè:
Dal fatto che, alzando la mano sinistra, l'immagine nello specchio alzerà la mano destra saremmo portati a credere che lo specchio capovolga le immagini da destra a sinistra, ma ciò non è vero. Esso rovescia le immagini da fronte a retro. I raggi di luce riflessi sono capovolti nella loro direzione, ma il loro moto verso destra o sinistra oppure verso l'alto o il basso rimane inalterato.
Osservandoci allo specchio percepiamo l'inversione destra - sinistra poichè la nostra immagine differisce da noi per l'inversione di una direzione, quella perpendicolare alla superficie dello specchio.
Anche se nel caso particolare dello specchio l'asse invertito è quello fronte-retro la nostra struttura fisica, sostanzialmente simmetrica rispetto all'asse destra-sinistra, ci porta ad associare l'inversione all'asse sbagliato.

Per renderci conto di questo fenomeno e uscire da questa illusione possiamo porci davanti allo specchio con due oggetti di colori diversi in mano: nella destra teniamo un pallina rossa, nella sinistra una blu.
Notiamo che l'immagine nello specchio tiene nella mano destra la pallina blu e non rossa!
Ora può essere più chiaro il fatto che le direzioni alto-basso e pallina blu-pallina rossa non vengono invertite, ma viene rovesciato soltanto l'asse fronte-retro.
Possiamo, quindi concludere che l'immagine nello specchio è la nostra, ma con il "verso" (fronte-retro invertito).
Analogamente, le lettere e le parole appaiono rovesciate nello specchio.
Come sappiamo, sulle ambulanze le scritte sono rovesciate, in modo da apparire in modo corretto quando sono lette nello specchietto retrovisore di un’automobile.


COSTRUZIONE DI IMMAGINI FORMATE DA UNO SPECCHIO PIANO
Consideriamo uno specchio piano e una sorgente di luce puntiforme P.
Applicando le leggi della riflessione, costruiamo due raggi riflessi provenienti da due raggi incidenti.
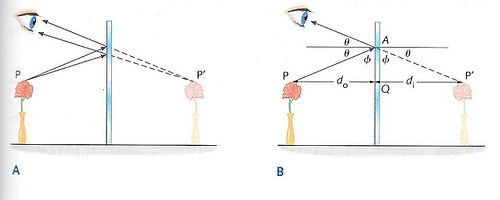
I raggi riflessi divergono, mentre i loro prolungamenti geometrici si incontrano nel punto P', simmetrico a P rispetto allo specchio. Infatti:
chiamiamo do la distanza di P dallo specchio e di la distanza di P' dallo specchio, consideriamo il raggio i1 proveniente da P, il quale viene riflesso ed entra nell’occhio dell’osservatore.
Consideriamo il prolungamento all’indietro del raggio riflesso fino a P';
per la seconda legge della riflessione abbiamo che, se l’angolo di incidenza nel punto A è ϑ, anche l’angolo di riflessione in A è ϑ.
Pertanto la linea retta che va dalla sorgente (P) all’immagine (P') taglia la normale con un angolo ϑ da entrambe le parti.
Gli angoli indicati con ϕ devono, quindi, essere uguali e i triangoli rettangoli PAQ e P’AQ, avendo il cateto AQ in comune e un angolo acuto uguale, sono necessariamente uguali.
Ne consegue che la distanza do è uguale alla distanza di.
Con un ragionamento analogo si può dimostrare che l’altezza dell’immagine è uguale all’altezza dell’oggetto.
Questo ragionamento può essere ripetuto per qualsiasi raggio riflesso.
Possiamo, quindi, concludere che i prolungamenti dei raggi riflessi s'intersecano nel punto P', simmetrico di P rispetto allo specchio.
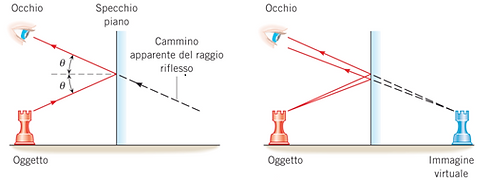
Una persona posta davanti allo specchio, infatti, ricevendo i raggi riflessi, avrà l'illusione che questi provengano da un punto oltre lo specchio. L'immagine di un oggetto di dimensioni finite si può ottenere ripetendo per ogni punto la costruzione appena esposta.
L'immagine vista attraverso uno specchio è detta immagine virtuale, in quanto sembra provenire da una direzione diversa rispetto all'oggetto e non può essere proiettata su uno schermo.
Anche se i raggi riflessi sembrano provenire dall’immagine, essi non hanno origine dietro lo specchio nella posizione in cui sembra che si trovi l’immagine. Poiché nessuno dei raggi luminosi riflessi proviene realmente dall’immagine, l’immagine formata da uno specchio piano è appunto chiamata immagine virtuale.
In generale possiamo classificare le immagini ottenute con dispositivi ottici in due gruppi fondamentali:
immagini reali e immagini virtuali.
- Si hanno immagini reali quando nella zona dello spazio dove i nostri occhi vedono l’immagine passano
realmente i raggi luminosi. Sono immagini reali per esempio quelle formate dagli specchi curvi.
- Si hanno, invece, immagini virtuali quando nella zona dello spazio dove i nostri occhi vedono l’immaginenon passano realmente i raggi luminosi.
Per esempio, l’immagine che vediamo in uno specchio, al di là dello specchio, è virtuale.
Possiamo, quindi, concludere che l’immagine formata da uno specchio piano sembra provenire da dietro lo specchio. Un raggio luminoso proveniente da un punto di un oggetto viene riflesso dallo specchio (l’angolo di incidenza è uguale all’angolo di riflessione) e colpisce il nostro occhio. Al nostro occhio appare come se provenisse da dietro lo specchio, in un punto situato lungo la retta tratteggiata della figura. In realtà, da ogni punto dell’oggetto partono raggi luminosi diretti in tutte le direzioni, ma solo una piccola parte di questi raggi viene intercettata dal nostro occhio.
La parte destra della figura mostra due raggi che partono dallo stesso punto dell’oggetto.
Tutti i raggi che hanno origine in un punto dell’oggetto, anche se incidono sullo specchio con angoli diversi, sembrano avere origine nello stesso punto dell’immagine dietro lo specchio (vedi le linee tratteggiate nella parte destra della figura). In conclusione, a ogni punto dell’oggetto corrisponde un solo punto dell’immagine: questo è il motivo per cui l’immagine prodotta da uno specchio piano appare nitida e non distorta.
SPECCHI SFERICI
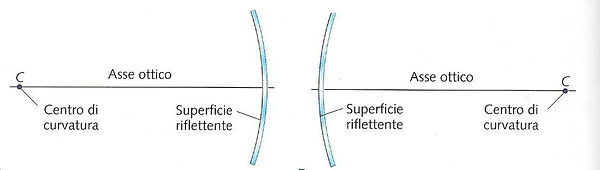
Uno specchio sferico ha la stessa forma di una calotta sferica. Se la superficie esterna di questa calotta è riflettente, allora lo specchio è convesso. Se la superficie riflettente è quella interna, lo specchio è concavo.
Il centro di curvatura è il centro della sfera alla quale appartiene la calotta e l’asse ottico è una retta che passa per il centro di curvatura e il punto medio dello specchio, è l'asse di simmetria dello specchio. Esso taglia lo specchio ad angolo retto.
La legge della riflessione che abbiamo enunciato per gli specchi piani vale anche per gli specchi sferici. In questo caso la normale è la perpendicolare al piano tangente alla superficie sferica nel punto di incidenza.
In figura possiamo osservare uno specchio convesso con indicato il suo centro di curvatura C, posto dalla stessa parte della superficie riflettente, e il suo asse ottico (o asse principale) e uno specchio concavo con il suo centro di curvatura, posto dalla parte opposta rispetto alla superficie riflettente e il suo asse ottico.
SPECCHI SFERICI CONCAVI
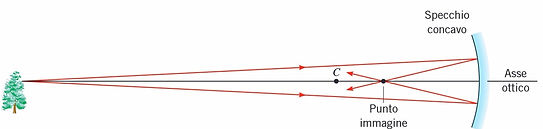
Consideriamo uno specchio sferico concavo, davanti al quale è presente un albero.
Un punto dell’albero si trova sull’asse ottico dello specchio e più lontano dallo specchio rispetto al centro di curvatura C.
Considerando solo raggi luminosi vicini all'asse ottico, abbiamo che i raggi riflessi convergono in un punto chiamato
punto immagine e poi proseguono il loro cammino divergendo dal punto immagine.
I raggi luminosi che provengono da questo punto sono riflessi dallo specchio secondo la legge della riflessione.
Si potrebbe pensare che in questo punto ci sia un oggetto da cui partono raggi luminosi.
Poiché dal punto immagine provengono realmente dei raggi luminosi, l’immagine è un’immagine reale.
Abbiamo considerato un albero più lontano dallo specchio rispetto a C, ma ad una distanza finita.
Se, invece, avessimo un albero a distanza infinita potremmo considerare i raggi luminosi provenienti da esso sostanzialmente paralleli tra loro e all’asse ottico.
Tali raggi, vicini all'asse ottico, sono detti raggi parassiali.
In questo caso, i raggi riflessi convergono in un punto detto punto focale F o fuoco dello specchio.
Quindi l'immagine dell'albero, o più in generale di un oggetto posto a distanza infinita dallo specchio concavo, si trova nel fuoco dello specchio.
La distanza tra il fuoco e il centro dello specchio è chiamata distanza focale f dello specchio stesso.
Il fuoco F di uno specchio concavo si trova a metà tra il centro di curvatura C e la superficie dello specchio.
In altre parole, la distanza focale f è pari alla metà del raggio di curvatura R:
NB: Abbiamo assunto che i raggi siano parassiali. Questa formula, infatti, non è valida per raggi distanti dall'asse ottico.
Ciò significa che la distanza tra l’asse principale dello specchio e i raggi incidenti dev'essere più piccola del raggio di curvatura R dello specchio.
Se i raggi avessero distanze dall’asse paragonabili al raggio di curvatura R , non tutti convergerebbero nel fuoco dopo essere stati riflessi; più un raggio è lontano dall’asse, più lontano passa dal fuoco.
In questo caso lo specchio produrrà un’immagine sfuocata, originando un effetto chiamato aberrazione sferica.
L’aberrazione sferica può essere minimizzata utilizzando uno specchio di altezza piccola rispetto al raggio di curvatura.
Un modo per eliminare l’aberrazione sferica ed ottenere, così, un'immagine nitida è costruire uno specchio parabolico.
Una delle proprietà della parabola è che i raggi paralleli al suo asse vengano riflessi in modo che passino tutti per lo stesso punto F, indipendentemente dalla loro distanza dall’asse.
Perciò uno specchio parabolico produce un’immagine nitida di tutti i raggi che entrano.
Per questo motivo gli specchi astronomici sono di forma parabolica, per dare la maggior luminosità possibile e le immagini più nitide possibili. Tali specchi sono, tuttavia, molto costosi.
SPECCHI SFERICI CONVESSI
Consideriamo uno specchio convesso e un fascio di luce diretto parallelamente al suo asse ottico.
Inoltre consideriamo solo raggi parassiali.
Dopo la riflessione contro lo specchio, i raggi divergono come se fossero originati da un singolo punto F dietro lo specchio.
Questo punto è il fuoco dello specchio convesso e la sua distanza dal centro dello specchio è la distanza focale f.
Anche la distanza focale di uno specchio convesso è uguale alla metà del raggio di curvatura, ma per convenzione è indicata con un segno negativo, per indicare che il fuoco giace dietro lo specchio:
COSTRUZIONE DELLE IMMAGINI PRODOTTE DA SPECCHI SFERICI:
Abbiamo visto che in uno specchio piano l’immagine formata è sempre dritta, della stessa misura dell’oggetto e alla stessa distanza dell’oggetto dallo specchio.
Nel caso di specchi sferici, l’immagine può essere sia dritta che ribaltata, sia ingrandita sia rimpicciolita, sia più vicina sia più lontana dell’oggetto dallo specchio.
Per trovare l’orientazione, la misura e la posizione dell’immagine di uno specchio sferico possiamo utilizzare due tecniche:
-
utilizzo dell’equazione degli specchi o equazione dei punti coniugati, la quale fornisce precise informazioni quantitative.
-
tracciamento dei raggi principali, il quale fornisce l'orientamento dell’immagine oltre che un’informazione qualitativa sulla sua posizione e grandezza. Se disegnato con cura, un diagramma dei raggi può fornire anche risultati quantitativi.
Tracciamento dei raggi principali
Il diagramma dei raggi permette di determinare sia la posizione dell’immagine sia le sue dimensioni semplicemente tenendo presente che i raggi parassiali provenienti da un punto dell’oggetto si intersecano dopo la riflessione nel corrispondente punto dell’immagine.
L’idea di base è quella di seguire il cammino di alcuni raggi di luce, che sono particolarmente significativi quando vengono riflessi da uno specchio e formano un’immagine.
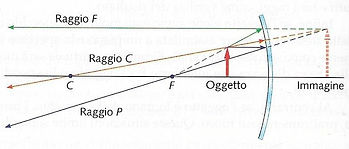
Ci sono tre raggi che hanno un comportamento particolarmente semplice e vengono maggiormente utilizzati in questo metodo:
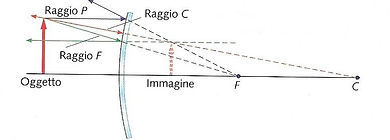
raggio C passante per il centro di curvatura, il quale interseca lo specchio ad angolo retto. Un raggio che si muove lungo questo percorso viene riflesso all’indietro per lo stesso cammino, in entrambi gli specchi.
raggio F, passante per il fuoco dello specchio. Esso viene riflesso parallelamente all’asse ottico nel caso di uno specchio concavo, mentre nel caso di uno specchio convesso esso si muove verso il fuoco finchè non viene riflesso dallo specchio e, dopodiché si muove parallelamente all’asse.
raggio P, parallelo all’asse ottico dello specchio. Esso viene riflesso in modo da passare per il fuoco di uno specchio concavo e lungo una linea che prolungata all’indietro passa per il fuoco in uno specchio convesso.
SPECCHI CONCAVI:
- Se l’oggetto è posto ad una distanza dallo specchio maggiore del raggio di curvatura otteniamo un’immagine capovolta, più vicina allo specchio e più piccola dell’oggetto. Inoltre, poiché la luce passa attraverso l’immagine, diciamo che essa è un’immagine reale.
- Se l’oggetto si avvicina al fuoco, un osservatore vedrà un’immagine grande e capovolta dell’oggetto lontano, davanti allo specchio.
- Se, invece, l’oggetto è posto tra il centro di curvatura e il fuoco otteniamo un’immagine capovolta, ma più lontana dallo specchio e più grande dell’oggetto; inoltre, anche in questo caso, l’immagine è reale , perché i raggi luminosi passano realmente per il punto immagine.
- Infine, se un oggetto è posto tra il fuoco e lo specchio, abbiamo che i tre raggi non si intersecano in un punto unico ma sono divergenti. Tuttavia i prolungamenti di questi raggi oltre lo specchio sembrano provenire da un unico punto, che appartiene all’immagine virtuale dell’oggetto. Questa immagine virtuale è diritta e ingrandita rispetto all’oggetto.
Questi disegni illustrano il seguente principio:
PRINCIPIO DI REVERSIBILITÀ DEI CAMMINI OTTICI
Se si inverte il verso di un raggio luminoso, il raggio ripercorre il cammino originale.
Questo principio ha una portata generale e non è quindi limitato alla riflessione da parte di uno specchio.
Generalmente questo tipo di specchi viene utilizzato per truccarsi, in quanto ponendo il viso tra lo specchio e il fuoco si ottiene un'immagine virtuale ingrandita.
SPECCHI CONVESSI:
Consideriamo uno specchio convesso, davanti al quale è collocato un oggetto.
Per determinare la posizione e le dimensioni dell’immagine formata da uno specchio convesso si può usare il metodo del diagramma dei raggi, ma bisogna tenere presente che il fuoco e il centro di curvatura di uno specchio convesso si trovano dietro la superficie riflettente, non davanti a essa.
Uno specchio convesso forma sempre immagini virtuali di un oggetto, indipendentemente dalla posizione dell'oggetto davanti allo specchio.
Se l’oggetto viene avvicinato molto allo specchio convesso, la superficie dello stesso può essere assimilata ad un piano e lo specchio si comporta essenzialmente come se fosse tale. Perciò l’immagine virtuale sarà dietro lo specchio, circa alla stessa distanza che intercorre tra l’oggetto e lo specchio, e sarà della stessa grandezza.
In questo caso otteniamo che l’immagine virtuale è diritta, più piccola dell’oggetto e localizzata tra lo specchio e il fuoco.
Al contrario, se l’oggetto è lontano dallo specchio, l’immagine virtuale è molto piccola, praticamente sul fuoco.
A causa della loro forma gli specchi sferici forniscono un campo visivo più ampio di quello di altri tipi di specchi. Per questo motivo sono spesso impiegati come apparati di sicurezza negli incroci stradali.
Uno specchio con un campo visivo ampio è necessario anche per fornire al conducente di un’automobile una buona visione di ciò che avviene dietro di lui. Per questo motivo gli specchietti retrovisori delle automobili sono in genere specchi convessi. Bisogna però ricordare che l’immagine virtuale formata da uno specchio sferico è rimpicciolita. Quindi l’automobile riflessa nello specchio retrovisore sembra più lontana di quello che è in realtà.
Equazione degli specchi
L’equazione degli specchi o equazione dei punti coniugati è una precisa relazione matematica tra la distanza dell’oggetto, do, quella dell’immagine dallo specchio, di, e la distanza focale, f.
Per uno specchio concavo vale:
NB: il segno della distanza dell’immagine (di) indica la parte, rispetto allo specchio, nella quale si trova l’immagine.
Notiamo, inoltre, che l’ equazione degli specchi è valida anche per gli specchi convessi, purché ci si ricordi che in questo caso la distanza focale (f) è negativa.
Oltre a stabilire la posizione dell’immagine di un oggetto formata da uno specchio, è importante valutare il suo ingrandimento G, cioè il rapporto tra l’altezza dell’immagine e quella dell’oggetto .
Il segno dell’ingrandimento fornisce l'orientamento dell’immagine: per convenzione, un’immagine rovesciata ha ingrandimento negativo, mentre un’immagine diritta ha ingrandimento positivo.
In particolare, vale .
Quindi se, per esempio, di e do sono entrambe positive allora l’ingrandimento è negativo e l’immagine è capovolta. Al contrario, se l’immagine è dietro allo specchio, così che di è negativa, l’ingrandimento è positivo e l’immagine è dritta.
Infine l’ingrandimento ci dà il fattore del quale è aumentata o diminuita la misura dell’immagine rispetto all’oggetto.
Nel caso particolare di un’immagine della stessa misura e orientazione dell’oggetto, come negli specchi piani, il valore dell’ingrandimento è 1.
Può essere utile sfruttare il programma Geogebra per visualizzare quanto detto finora.
Cliccando sul link sottostante è possibile studiare la formazione di un'immagine prodotta da uno specchio.
Muovendo il comando in alto, il quale fa variare la curvatura, è possibile studiare i casi di specchio
convesso, specchio piano e specchio concavo.
RIEPILOGO DELLA CONVENZIONE SUI SEGNI PER GLI SPECCHI SFERICI
Riepiloghiamo le convenzioni sui segni usate nell’equazione dei punti coniugati e nell’equazione dell’ingrandimento. Queste convenzioni valgono sia per gli specchi concavi sia per quelli convessi.
Una proposta di attività in classe
Dopo aver affrontato la parte sugli specchi e la formazione delle immagini, i ragazzi possono osservare in modo pratico quanto detto svolgendo la seguente attività. Questa può essere proposta come gioco a squadre.
Si dividono gli studenti in gruppi di 4 e ad ogni gruppo si consegna uno specchio concavo, una candela, un piatto e un rotolo di spago.
Ogni gruppo procede attaccando la candela sul piatto e fissando un pezzo di spago al bordo, in modo che lo stesso possa essere trascinato. Si pone questo apparato sul pavimento.
Lo spago viene steso in linea retta e dopo un tratto abbastanza lungo viene posizionato lo specchio concavo. È possibile tracciare una linea guida che collega i due oggetti con il nastro adesivo.
Accendendo la candela e tirando lo spago, mantenendo la direzione rettilinea, si può osservare come inizialmente l’immagine della candela nello specchio sia rimpicciolita e capovolta, mentre dopo aver superato il fuoco dello specchio essa risulti dritta e ingrandita.
Si possono invitare gli studenti a filmare l’esperimento e descriverlo. La squadra che descriverà in modo migliore e più efficace il meccanismo della formazione di un’immagine da parte di uno specchio concavo, sarà la vincitrice del gioco.
